GPSS - Introduction and Barber Shop Simulation
We’ll now look at GPSS, a simulation language included in MTS. Due to the specialized nature of this language I’ll only devote a single post to it - but it’s a very interesting language, so let’s dive in!
General Purpose Simulation System
GPSS, General Purpose Simulation System, is a language to simulate discrete systems to see how they perform over time. Sample uses include modeling a checkout at a supermarket or how a manufacturing assembly line will work. The programmer defines how transactions are created (eg a shopper), what resources are available (eg how many checkouts and how long they take to process) and how transactions move through the system. When run, it simulates a clock and processes these transactions, giving output that shows the performance of the system, eg how long on average a shopper had to queue for and how busy the checkouts where during a simulated day.
GPSS on MTS
GPSS was created by Geoffrey Gordon in around 1961 and was originally implemented on IBM systems. The version we have on MTS, GPSS/360, is available as *GPSS. Later versions of GPSS such as GPSS/H did run on MTS and may be available in future distributions (see this message at the MTS Archive).
Prerequisites
No special installation instructions to get this language running - just do the standard D6.0 setup as described in this guide and then sign on as a regular user such as ST01.
A barber shop simulator
As a sample program, let’s look at the Barber Shop: First Model from General Purpose Simulation System/360: Introductory Concepts and Case Studies by Thomas J. Schriber.
We are modeling a barber shop with the following qualities:
- The shop contains one barber and one barber’s chair, open for eight hours in a day.
- Customers arrive on average every 18 minutes, with the arrival time varying between 12 and 24 minutes.
- If the barber is busy, the customer will wait in a queue.
- Once the barber is free, the next customer will have a haircut.
- Each haircut takes between 12 and 18 minutes, with the average being 15 minutes.
- Once the haircut is done, the customer will leave the shop.
We want to answer these questions:
- How utilised is the barber through the day?
- How long does the queue get?
- On average, how long does a customer have to wait.
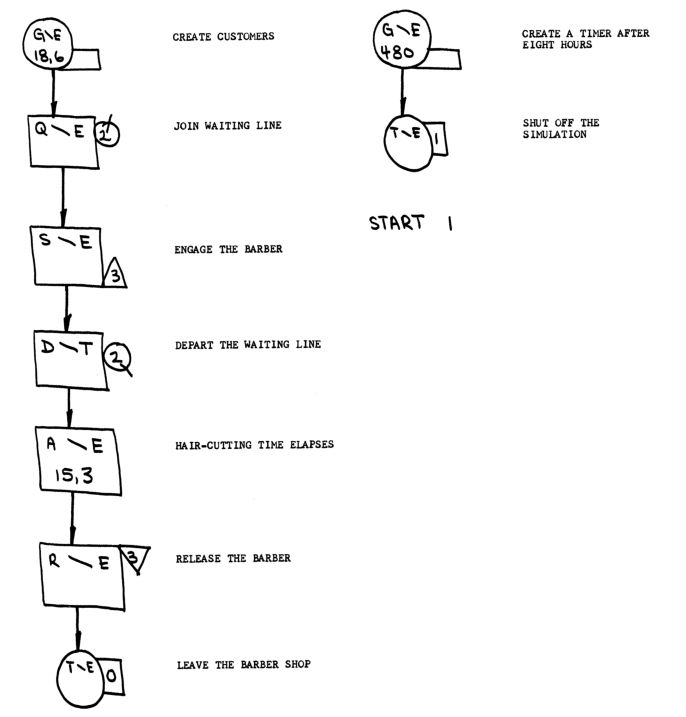
The manual uses a block diagram notation to show how this is simulated - you can see this at the top of this page. The equivalent GPSS program looks like this:
SIMULATE
GENERATE 18,6 CREATE CUSTOMERS
QUEUE 2 CUSTOMERS QUEUE UP IF NECESSARY
SEIZE 3 ENGAGE THE BARBER WHEN HE BECOMES AVAILABLE
DEPART 2 CUSTOMER LEAVES THE QUEUE
ADVANCE 15,3 CUSTOMER GETS HIS HAIR CUT
RELEASE 3 RELEASE THE BARBER
TERMINATE 0 LEAVE THE BARBER SHOP
GENERATE 480 GENERATE A TIMER AFTER 8 HOURS OF SIMULATED TIME
*
TERMINATE 1 SHUT OFF THE RUN
START 1 CARRY OUT THE SIMULATION
END RETURN CONTROL TO THE OPERATING SYSTEM
The text at the end of each line is a comment; starting a line with * means the rest of the line is a comment; we use this just to separate the two parts of the program as explained below.
GPSS works in units rather than absolute time, so we shall say that 1 time unit is equal to 1 minute. Programs can be read from top to bottom: the simulator runs by advancing the clock one time unit and working out where transactions are in the system.
The first line, SIMULATE, denotes the start of the code.
GENERATE 18,6 means generate a transaction - a barber shop customer - every 18 minutes ± 6 minutes.
QUEUE 2 defines a queue with ID 2, denoting the queue where customers will wait.
SEIZE 3 defines a facility with ID 3. The facility is the barber and this line means if the barber is free, the next customer occupies the barber until released.
DEPART 2 says that the customer leaves the queue when occupying the barber.
ADVANCE 15,3 means that transactions in this state only move on after 15 minutes ± 3 minutes - modeling the time taken for a haircut. After that RELEASE 3 shows that the customer no longer occupies the barber and TERMINATE 0 ends the transaction, showing that the customer has left the shop.
That is all that is needed for the basic simulation, but if run like this it would never stop, as we have not modeled the 8 hour period the shop is open.
To do this we generate a new transaction with GENERATE 480, which means generate a transaction after 480 minutes, ie 8 hours. The next line, TERMINATE 1, stops the simulation after this transaction is generated.
With that done, the last two lines start the simulator and returns control to MTS when it is done.
Running the program using *GPSS
*GPSS takes the input file on scards and outputs to *sink* by default. Assuming the simulation defined above is stored in barb1.gpss, this is how it would look:
We start off with the program listing, where GPSS denotes which lines are components of the simulation with a block ID. So GENERATE 18,6 is on line 3 but is block 1.
$run *gpss scards=barb1.gpss
Execution begins 16:07:50
GPSS/360 VERSION 1 MODIFICATION LEVEL 4 MTS MODEL (AN104) 16:07:50 11-03-17
LINE# CARD# BLOCK# *LOC OPERATION A,B,C,D,E,F,G COMMENTS
1.000 1 SIMULATE
2.000 2 * BARBER SHOP SIMULATOR
3.000 3 1 GENERATE 18,6 CREATE CUSTOMERS
4.000 4 2 QUEUE 2 CUSTOMERS QUEUE UP IF NECESSARY
5.000 5 3 SEIZE 3 ENGAGE THE BARBER WHEN HE BECOMES AVAILABLE
6.000 6 4 DEPART 2 CUSTOMER LEAVES THE QUEUE
7.000 7 5 ADVANCE 15,3 CUSTOMER GETS HIS HAIR CUT
8.000 8 6 RELEASE 3 RELEASE THE BARBER
9.000 9 7 TERMINATE 0 LEAVE THE BARBER SHOP
10.000 10 *
11.000 11 8 GENERATE 480 GENERATE A TIMER AFTER 8 HOURS OF SIMULATED
12.000 12 9 TERMINATE 1 SHUT OFF THE RUN
13.000 13 START 1 CARRY OUT THE SIMULATION
14.000 14 END RETURN CONTROL TO THE OPERATING SYSTEM
Next, GPSS shows how many transactions were in each block at the end of the simulation and in total.
RELATIVE CLOCK 480 ABSOLUTE CLOCK 480
BLOCK COUNTS
BLOCK CURRENT TOTAL BLOCK CURRENT TOTAL BLOCK CURRENT TOTAL BLOCK CURRENT TOTAL BLOCK CURRENT TOTAL
1 0 27
2 0 27
3 0 27
4 0 27
5 1 27
6 0 26
7 0 26
8 0 1
9 0 1
We can see that 27 transactions were generated in block 1, which means 27 customers entered the shop during the day. Blocks 8 and 9 had 1 transaction, which is expected as this was the timing transaction. Why does block 5 have one current transaction while all others are zero? Block 5 is the ADVANCE statement, representing the haircut, and this means one customer was in the chair at the end of the simulated day.
GPSS then prints out statistics on the facility, or the barber in our simulation:
FACILITY AVERAGE NUMBER AVERAGE SEIZING PREEMPTING
UTILIZATION ENTRIES TIME/TRAN TRANS. NO. TRANS. NO.
3 .816 27 14.518 1
So our barber was used 81.6% of the day, and each haircut took on average 14.518 minutes.
We then see details of the queue:
QUEUE MAXIMUM AVERAGE TOTAL ZERO PERCENT AVERAGE $AVERAGE TABLE CURRENT
CONTENTS CONTENTS ENTRIES ENTRIES ZEROS TIME/TRANS TIME/TRANS NUMBER CONTENTS
2 1 .085 27 16 59.2 1.518 3.727
$AVERAGE TIME/TRANS = AVERAGE TIME/TRANS EXCLUDING ZERO ENTRIES
MAXIMUM CONTENTS means there was never more than one customer in the queue. Although 27 customers entered the queue, 16 were zero entries - this means they entered and immediately left the queue, ie the barber was unoccupied when they entered the shop. For those that did wait in the queue, the average wait was 3.727 minutes; including the zero entries, the average time for all customers to wait was 1.518 minutes.
Finally, GPSS prints usage statistics and exits:
CPU TIME USED (SECONDS)
ASSEMBLY: .001
TOTAL BLOCK EXECUTIONS: 189
MSEC/BLOCK AVG CPU TIME: .003
Execution terminated 16:07:50 T=0.004 RC=0 $0.00
It’s interesting to compare this to the printout in the manual from 1968. Our run took 0.004 seconds of CPU time, compared to 4.5 seconds then. And of course our run had no charge, whereas the run from 1968 would have cost 41¢.
The manual goes on to refine the model further - dealing with the customer left in the chair, and simulating more complex scenarios - but we will leave it at that for now.
Further information
Full source code for the program described above can be found on github.
The original IBM manuals for GPSS/360 don’t appear to be available anywhere online. The best reference I’ve found is, as mentioned above, General Purpose Simulation System/360: Introductory Concepts and Case Studies at Deepblue.
Modern implementations of GPSS on Windows are sold by Wolverine Software and Minuteman Software; both offer a free student version with limited model sizes.
Several other simulation languages have been created, eg Simula; a list of languages for discrete event simulations can be found at Wikipedia.